„Ich kann ja da gerade eh nix ändern.“ Diesen Satz habe ich in letzter Zeit im Zusammenhang mit der aktuellen Corona-Krise schon oft gehört. Warum das nicht ganz richtig ist, erfährst Du in meinem neuen Video. Das ist mein kleiner Beitrag, damit wir das alle überstehen:
Lieber Niesnutzer!
Mit diesem Video möchte ich Dich nicht bevormunden oder so. Ich versuche einfach, zu schützen, was mir wichtig ist. Und da gehören meine Niesnutzer natürlich dazu, was Du schon daran siehst, welchen Aufwand ich betreibe, um die Lehrvideos für Euch zu erstelle (Wie ihr vermutlich wisst, verdiene ich ja kein Geld damit – ich mache das, weil ich im Leben viel Glück hatte und der Welt etwas zurück geben möchte). Also bitte sei offen, wenn Du das Video schaust und bilde Dir Deine eigene Meinung zum Thema.
Viele Grüße,
Andreas Nies
Untertitel für Hörgeschädigte:
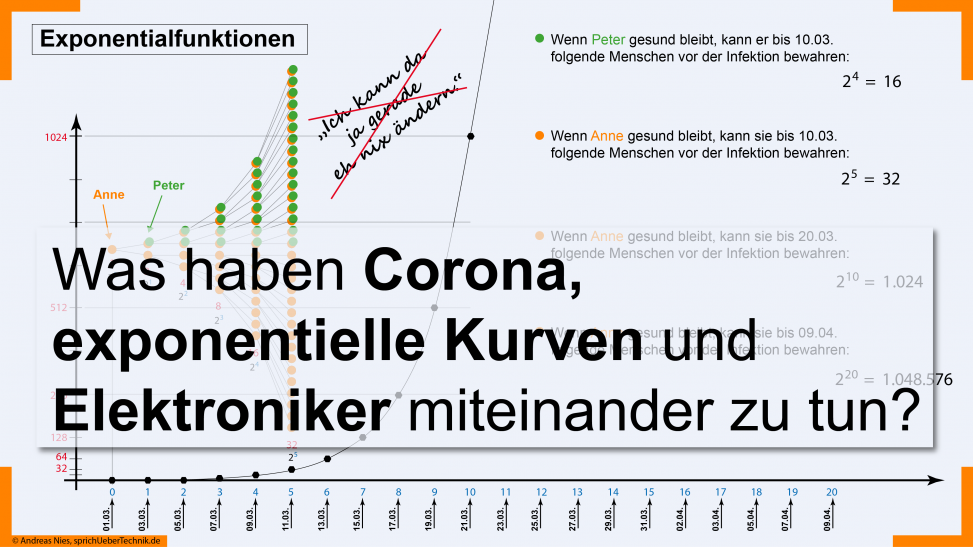
„Ich kann ja da gerade eh nix ändern.“ Diesen Satz habe ich in den letzten Tagen im Zusammenhang mit der aktuellen Corona-Krise schon sehr oft gehört. Warum das aus meiner Sicht nicht ganz richtig ist, erfährst Du in diesem Video. [Musik] Hallo lieber Niesnutzer! Schön, dass Du wieder da bist. Heute geht’s bei mir um Exponentialfunktionen und es wird Dich vielleicht überraschen, aber Exponentialfunktionen haben auch was mit dem Beruf des Elektronikers zu tun. Dieser kleine Punkt, das ist die Anne. Anne geht am 01.03.2020 (das Datum ist willkürlich gewählt) auf die Straße und steckt sich dort mit dem Corona Virus an. Man liest ja mittlerweile häufiger in den Medien, dass alle zwei Tage sich die Anzahl der infizierten Menschen gerade verdoppelt. Das heißt, wir hätten also zwei Tage später zwei infizierte Personen, die auf Anne zurückzuführen wären. Das ist nämlich die Anne selbst und eine neue infizierte Person… Wie sieht das Ganze jetzt nach zwei weiteren Tagen aus? Dann schreiben wir den 5. März und wir hätten schon 4 Infektionen – alle auf Anne zurückzuführen. Nennen wir den hier oben, der davon Anne angesteckt wurde einfach mal den Peter. Wie geht es jetzt weiter? Weitere zwei Tage später hat sich die Anzahl wieder verdoppelt das sind also jetzt insgesamt acht infizierte Personen. Ja so weiter geht es dann. Weitere 2 Tage weiter und dann haben wir hier schon 16 angesteckte Personen. Und noch mal 2 Tage weiter: Das wäre dann, am 11. März, da hätten wir dann schon 32 angesteckten Personen und 2 Tage später am 13.03. – freitag der dreizehnte übrigens – da wären es jetzt schon 64 infizierte Personen mehr als vorher. Und jetzt sieht man schon das erste Problem mit diesen exponentiellen Funktionen diese 64 Punkte, die habe ich auf meine Folie hier gar nicht mehr drauf gekriegt. Deshalb habe ich das auch erst mal sein lassen und hatte dazu eine andere Idee. Aber mehr dazu später. Jetzt schauen wir uns das erste mal an. Wie viele von diesen Personen sind jetzt auf die Anne zurück zu führen und wie viele von diesen Personen sind jetzt auf den Peter zurückzuführen? Der Peter der hat zuerst eine weitere Person angesteckt dann haben die jeweils wieder jemanden angesteckt und alles in allem sind das am Ende hier 16 Personen. Wir können also schon mal festhalten: Wenn Peter gesund geblieben wäre, dann hätte er die folgende Anzahl von Menschen vor der Infektion bewahren können: 2 hoch 4 also 16 Das mit dem 2 hoch 4, das kommt Euch vielleicht bekannt vor aus Eurer Ausbildung. Und das ist auch genau das, was diese Kurve hier mit dem Beruf des Elektronikers zu tun hat: 1,2,4,8,16,32 … diese Folge von Zahlen, die könnte Euch bekannt vorkommen. Und zwar aus dem Binärsystem. Da hat man nämlich auch zwei hoch 0, 1, 2, 3 etc. und das ist dann 1, 2, 4, 8 etc. Schauen wir uns das Gleiche mal für die Anne an. Die Anne ist ja diese orangene Person hier vorne. Die hat erst mal 2, dann 4, dann 8, dann 16, dann 32 Personen in ihrer Infektionskette – inklusive sich selbst. Und wir können also an der Stelle festhalten: Wenn Anne zuhause geblieben wäre, dann hätte sie bis zum 10.3 2^5, also 32 Menschen, inklusive sich selbst, retten können. Na ja jetzt schreitet die Zeit aber natürlich weiterhin fort und in diesem Koordinatensystem habe ich auf der X-Achse hier unten die Anzahl der vergangenen Intervalle, also das sind immer 2-Tages-Intervalle und auf der Y-Achse, da habe ich jetzt die Anzahl der Infektionen und jetzt müssen wir im Prinzip nur noch die Punkte in das Diagramm einzeichnen. Die 2 hoch 0, die käme ja hier hin. Da müssen wir also eine 1 einzeichnen und wenn hier 1024 sind .. da sind 32 .. hier die 16 sieht man gerade noch so, aber die 1, die sieht man im Prinzip da unten gar nicht. Also 2 hoch 0, das wäre fast genau auf der Nulllinie u.s.w. 2 hoch 6; 2 hoch 7; 2 hoch acht; kannste auf dem Taschenrechner mal mit tippen: die 256. Und 2 hoch und 9 sind die 512. Das geht jetzt richtig steil bergauf und die 2 hoch 10 hier oben, da haben wir schon die 1024 erreicht und jetzt sieht man schon das nächste Problem mit diesen exponentiellen Kurven: Auch in der Exponential-Darstellung als Kurve hier im Koordinatensystem sieht man, dass die sehr schnell hier oben aus dem Bild heraus wandert … das liegt daran, dass so eine exponentielle Kurve einfach sehr sehr schnell steigt. Anhand dessen, was wir an dieser Kurve ablesen können, können wir sagen: Am 21. – also nach 10 intervallen oder 20 Tagen (also hier hört der 20. auf, hier fängt der 21. an) also da hätten wir weil Anne sich infiziert hat: 2 hoch 10 Infizierte, inklusive der Anne. Und das wären dann 1024. das ist schon eine ordentliche große Sporthalle voll und wir haben ja hier unten noch eine X-Achse die noch ein bisschen weiter geht. Hier unten sind wir bei 2 hoch 20 und das kannst Du in Deinen Taschenrechner eintippen, wieviel 2 hoch 20 sind: Dann haben wir nämlich genau die Zahl. Nach 20 Intervallen, also nach 40 Tagen, hätte die Anne also 2 hoch 20 = 1.048.576 Menschen vor der Infektion bewahren können. Naja und jetzt weißt Du auch, warum ich ganz am Anfang gesagt habe: Das hier mit dem: „Ich kann da ja gerade eh nichts ändern.“ .. das glaube ich nicht. Was können wir also jetzt tun? M. E. ist das Beste – wenn man die Wahl hat – einfach zu Hause zu bleiben. In der nächsten Zeit sollte jedes Mal, wenn man vor die Tür geht die Frage sein: Tue ich das jetzt um irgendetwas Gutes zu tun, (z.B. älteren Menschen zu helfen oder Menschen, die mich gerade brauchen, weil sie krank sind und beispielsweise für die einzukaufen) … oder tue ich das aus rein egoistischen Gründen für mein persönliches Vergnügen? Du könntest in der zeit natürlich ein paar Elektro-Aufgaben rechnen, denn die nächste Prüfung kommt ja wahrscheinlich trotzdem und Du könntest in dieser Zeit mit allen Menschen sprechen, die Du gerne hast, um sie auch davon zu überzeugen, jetzt mal für eine begrenzte Zeitdauer zu Hause zu bleiben, um so vielleicht 1 Million Infektionen in einem Zeitraum von 40 Tagen zu verhindern. Und jetzt: Schreib mir doch vielleicht mal unten in die Kommentare, was Du noch für Ideen hast, wie man der Menschheit am besten aus dieser Krise heraus helfen kann… Vielen Dank fürs Zuhören, lieber Niesnutzer und tu mir einen Gefallen: bleib gesund! Tschüss bis nächstes Mal. [Musik]

Schreibe einen Kommentar
Du musst angemeldet sein, um einen Kommentar abzugeben.